「初期値がほんの少し違うだけで、未来が大きく変わる」――
カオス理論の象徴である バタフライ効果 を、ブラウザ上でダイナミックに体験できるウェブアプリが登場しました。その名も 「Strange Attractors」。
開発者はエンジニアの Shashank Tomar氏。Three.js を活用し、数十万〜数百万もの粒子がリアルタイムで軌道を描く様子を3D表示します。
見た目はアート、裏側は高度な数式とGPU活用。
この記事では、アプリの魅力と背景にあるカオス理論、さらには実世界とのつながりまで、わかりやすく解説していきます。

🎨 無数の点がつくる、謎めいた幾何学模様
アプリを開くと、立方体状に配置された無数の点が表示されます。
再生ボタンを押すと、その点が 奇妙な軌跡を描きながら動き始め、時間が経つほど複雑な模様 に変化していきます。
この軌跡こそが ストレンジアトラクター(Strange Attractor)。
- ある点に収束するわけでもない
- 発散して消えるわけでもない
- ずっと複雑な形を描き続ける
まるで、法則性と無秩序が同居した“不思議な秩序”が目の前に現れます。

右下にある2つのボタンのうち、右にある再生ボタンをクリックするとアニメーションが再生され、時間経過で各点の座標が変化します。左の矢印ボタンで、アニメーションを最初からリプレイできます。

ストレンジアトラクターは左側にあるメニューから選択できます。
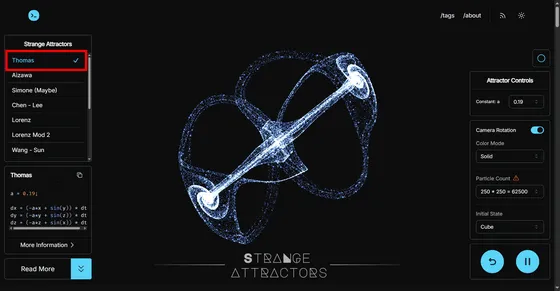
「More information」をクリックすることで、微分方程式の詳細を見ることが可能。

🪄 ストレンジアトラクターとは?
点の位置は、微分方程式で定義されます。
通常の力学系では、解は 安定点や周期軌道に収束 しますが、カオス系では違います。
👉 わずかな違いが、最終的に巨大な違いを生む
これがカオス理論のコア。
アトラクターは安定しないにも関わらず、ある領域に“とどまり続ける”ため、複雑で美しい形になるのです。
⚙️ 代表的なアトラクターが選べる
左メニューから以下のアトラクターを切り替えられます。
- Thomas
- Aizawa
- Lorenz(ローレンツ)
たとえば Thomas 系の場合は次の方程式:
dx = (-a x + sin(y)) dt
dy = (-a y + sin(z)) dt
dz = (-a z + sin(x)) dt
定数 a を少し変えるだけで、見た目は劇的に変化します。
これはまさしく バタフライ効果の視覚化。
🌀 Aizawaアトラクターは渦の芸術
Aizawaは3つの定数 a・b・c を使うタイプ。
画面内で点が渦を巻き、まるで銀河のような模様が浮かび上がります。
パラメーターを変えるたびに、
- ゆったりとしたスパイラル
- 激しい乱れ
- ねじれたリング状の構造
など、まったく異なる世界が出現します。
🌈 点の色や表示数も変更可能
以下の項目を自由に調整できます。
- Particle Count(点の数)
- Color(色)
- Initial State(初期配置)
初期配置は2種類:
- Cube(立方体)
- Sphere Surface(球の表面)
GPU負荷が上がるので、PCスペックに応じて調整すると快適です。
🚀 爆速処理を支える「ピンポンレンダリング」
数百万点の位置をリアルタイム計算するには、CPUでは追いつきません。
そこで使われているのが ピンポンレンダリング という技術。
仕組みはこうです👇
- GPUに データ置き場A と データ置き場B を用意
- Aを読み → 計算 → Bへ書き込み
- 次フレームは逆
- A ←→ B を高速で切り替え続ける
CPU↔GPU間の転送をなくせるため、驚くほど高速に描画できます。
この仕組みはゲームやWebGLの世界で広く使われる最適化テクニックです。
🌍 バタフライ効果は本当に存在するのか?
「バタフライ効果」という言葉はロマンがありますが、科学的な裏付けもあります。
- 近年の研究では、ミツバチの群れが局所的な気象に影響を与える 可能性が指摘されています。
- さらに、カオス的なシステムであっても 機械学習を使えば高精度に予測できる という研究も進んでいます。
気象予報・金融市場・感染症モデルなど、
カオス理論は現代のシミュレーション分野で依然として重要な役割を担っています。
🔍 なぜ今、ストレンジアトラクターが注目されているのか?
理由は3つ:
① GPUによる高速計算が一般化した
ブラウザでも数百万点をリアルタイム処理。
昔は研究室のスーパーコンピューターだった領域 が一般化しました。
② 可視化が圧倒的に簡単になった
Three.js、WebGL、Shaderの普及により、
「数学 → そのままアート」 という体験ができるようになりました。
③ 教育・研究用途に最適
カオス理論は難解ですが、
見れば直感的に理解できる。
- 大学の教材
- STEM教育
- ジェネラティブアート
など応用範囲が広がっています。
🧭 まとめ:数学がアートになる瞬間
Strange Attractors の魅力は、
純粋な数学が、リアルタイムで美しいアートになる瞬間を見せてくれること です。
- 初期値のわずかな違いで大きく変化する
- 複雑なのに、どこか秩序がある
- 動いているだけでずっと見てしまう
カオス理論は「難しい概念」と思われがちですが、視覚化すると驚くほど直感的。
ブラウザで動くので、ぜひ触ってみてください。
きっと、“数学が生きている”感覚を味わえるはずです。
